昨日の記事で得られた東方キャラ同士の関連性の強さ(NPMI)を使って、Isomapという手法でキャラを二次元上に配置して可視化します
東方キャラの関連性の強さをニコニコ動画の動画数で測ってみた - 唯物是真 @Scaled_Wurm
Isomapの概要
Isomapは非線形次元削減、あるいは多様体学習の手法の一つです
非線形次元削減では、与えられたデータの元の次元数での情報をできるだけ失わないように、より低次元に埋め込みます
多くの手法では元のデータでの近傍(近いデータ点)や距離を保存するような埋め込みを行います
最近流行りのニューラルネットワークも内部では非線形次元削減的なことをしていて、単語を密なベクトルに変換するword2vecなどは、単語同士の意味の足し算引き算がうまくいくことがあっておもしろいです
ちなみにscikit-learnの多様体学習の説明は、実行結果の図や計算量などいろいろのっていてわかりやすいです
Isomapのアルゴリズム
Isomapでは以下のような処理を行います
- データ点のk近傍(k番目までの近いデータ点)を辺でつないだグラフを作る(グラフ理論とかのグラフです)
- 辺はデータ点の距離で重み付けします
- グラフ上でのデータ点同士の最短距離を測る
- 上で計算した距離との誤差が小さいような低次元の埋め込みを求める
簡単な例を示します
以下の様なデータが与えられたとします

これの近傍をつなぐと次のようになります
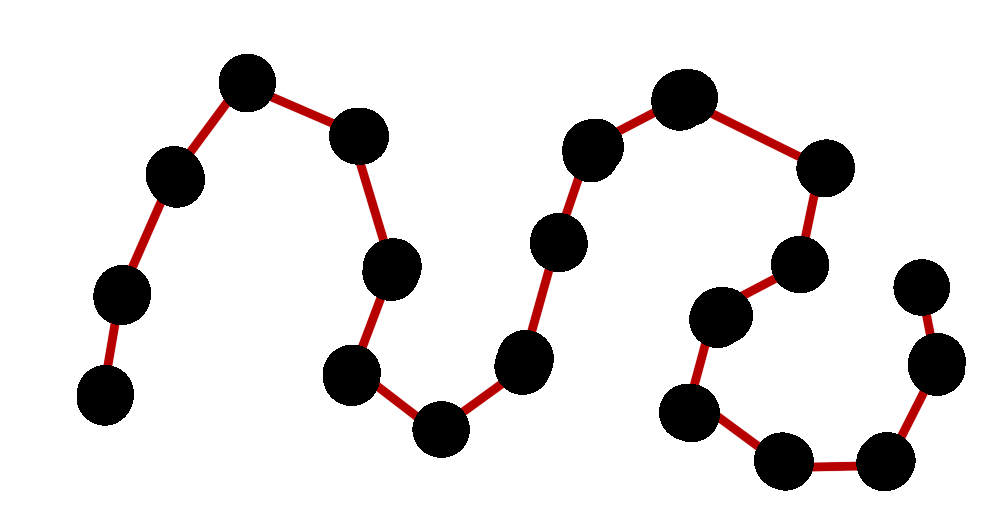
これは曲がりくねった曲線上の点であると解釈することができ、点の近傍の関係を保ったまま1次元に埋め込むことができます
このようにデータをより低次元の構造で表せる的なのが多様体の考え方です(?)
非線形次元削減では距離の決め方や近傍の定義がとても重要になります
例えばベクトルの次元ごとに値の範囲の大小が違うと悪影響があったりします(絶対値の大きな次元のほうがユークリッド距離では大きな影響を与える)
東方キャラを2次元に埋め込む
基本的な流れは、まず1次元1キャラで対応付けてキャラごとに相手キャラとのNPMIの値のベクトルを作ります
次にIsomapを適用して2次元に埋め込んで可視化します
scikit-learnのIsomapの実装はユークリッド距離しか使えないので、ベクトルの方を工夫してうまく似たキャラが近くになるようにします
具体的には各キャラのベクトルごとに、NPMIが上位の相手キャラだけの値を入れて、他のキャラ(次元)の値は0とします
NPMIが高いキャラ同士が近くなって欲しいのでこのようなベクトルにします
また同様の理由でIsomapで近傍グラフを作るときのkの数は3としました
結果
クリックすると拡大した画像が表示されます(100件以上の動画に出現したキャラしか使っていないので、見つからないキャラについては、お察しください)
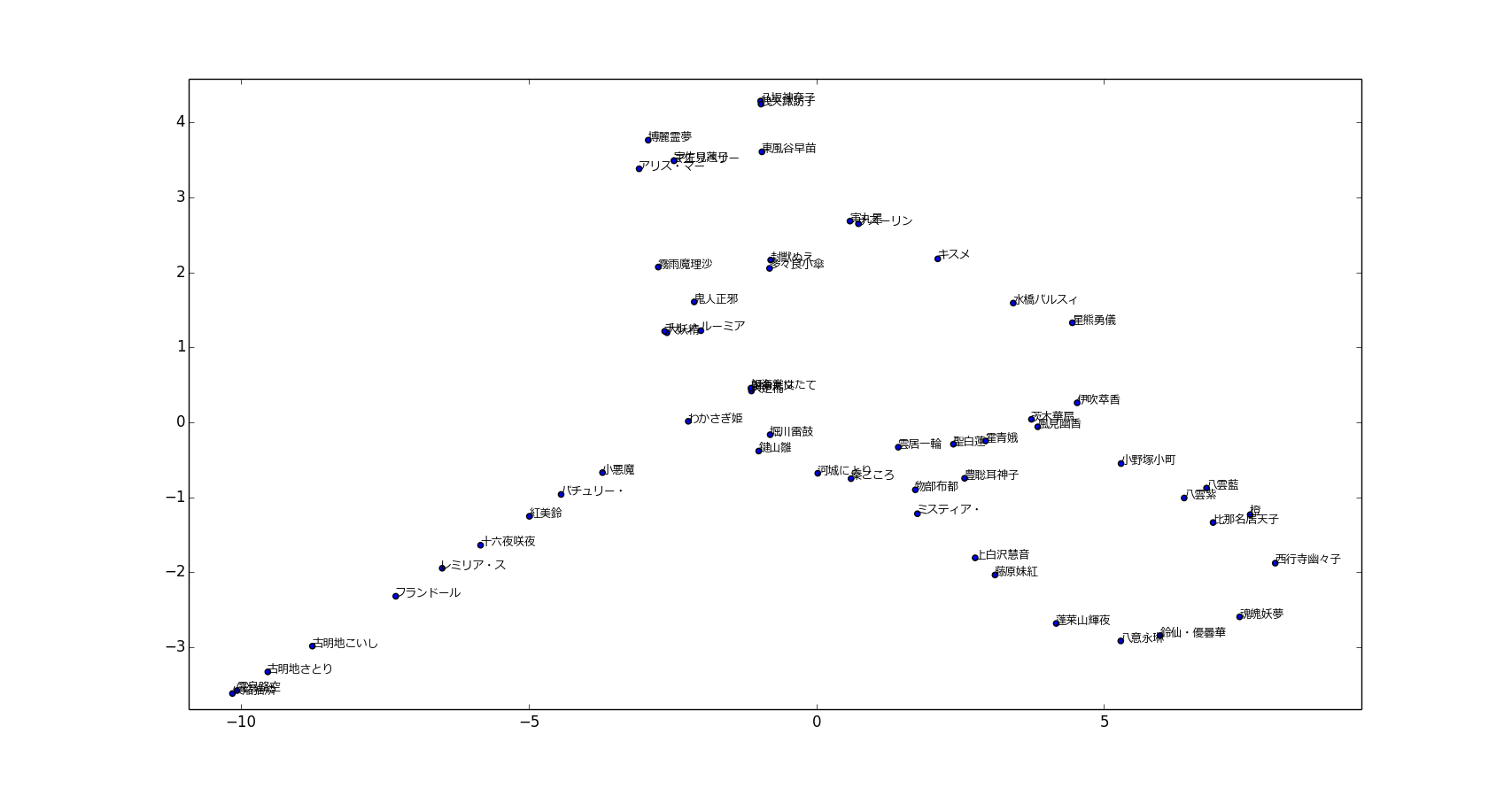
各キャラの近くのキャラ同士はだいたい関係のあるキャラ同士が集まっています
紅魔館などが離れたところに島を形成しているのは、グループ内だけで近傍の関係がほぼまとまっていたからだと考えられます
可視化としては全体的にはあまりよい見た目ではありませんが、データ点が重ならないようにばらけさせるような処理があるわけではないので、こんな感じになります
参考
Isomapの説明は日本語だと以下のスライドがわかりやすいと思います
Rでisomap(多様体学習のはなし)
Isomapと似た方法で多次元尺度構成法(Multidimensional scaling, MDS)という手法があります
これはIsomapとは違い、元の次元数でのすべてのデータ点の間の距離を保存するような埋め込みを行う手法です
ソースコード
後で足します