LTV(lifetime value)という顧客(ユーザー)が将来的に使う金額を予測しようという話があります
前に以下の記事でも書きましたが、月額課金制のサービスだと粗い推定として解約率を一定とみなして解約率の逆数を平均継続期間としてLTVを計算したりしています
sucrose.hatenablog.com
LTVがわかれば、例えばLTVが5000円のユーザーを獲得するのにコストとして3000円をかけるとユーザーを一人獲得するごとに2000円ずつ利益が出る、と言った計算ができます
新規ユーザーのLTVを既存ユーザー全体の解約率の逆数で計算しているのを見かけて「新規ユーザーの解約率って既存ユーザー全体の解約率とは全然合わないのでは?」と思ったので簡単に計算してみました(先月以前に契約した解約率の低いユーザーが残っているので新規ユーザーの解約率よりも全体の解約率は下がるはず?)
シミュレーション
設定
極端な例として、毎月以下の200人のユーザーが新規に月額1000円の課金制のサービスに契約するとしてシミュレーションしてみます
- 月ごとの解約率が10%のユーザー100人
- 月ごとの解約率が50%のユーザー100人
解約は必ず月末に発生し、ある月に契約したユーザーの解約は契約したその月から発生するとします
月ごとの解約率が10%の新規ユーザーの解約率の逆数でLTVを求めると\(1000 \times \frac{1}{0.1} = 10000\)
月ごとの解約率が50%の新規ユーザーの解約率の逆数でLTVを求めると\(1000 \times \frac{1}{0.5} = 2000\)
上記の2群100人ずつの平均のLTVは\(\frac{10000 \times 100 + 2000 \times 100}{200} = 6000\)となります
ちなみに上の方にも貼った以下の記事に書いたように全体の解約率の逆数からLTVを計算すると個々のユーザーの解約率の逆数から計算したLTVの平均とは全然違う値になるので注意が必要かもしれません(?)
今回の場合、解約率の平均は\(\frac{0.1 \times 100 + 0.5 \times 100}{200} = 0.3\)なので、解約率の逆数でLTVを求めると\(1000 \times \frac{1}{0.3} \approx 3333\)
結果
上記の条件でシミュレーションを動かして、月ごとのユーザーの人数、解約率、LTVについて計算してグラフを書いてみました(60ヶ月まで10000回の平均)
解約率(churn rate?)の定義は解約したユーザー数を分母で割るというものですが、分母となるユーザー数は月の途中で変わってしまうので、分母を単純に月末にいたユーザー数にしたり、月初と月末のユーザー数の平均にしたりいろいろなバリエーションがあります
計算が楽なので、今回は月末にいたユーザー数(その月に解約したユーザーも含む)を分母とします
グラフ
ユーザー数は月が経過すると、解約率ごとに一定の値に収束しているのがわかる(その月に解約した人数は含んでいません)
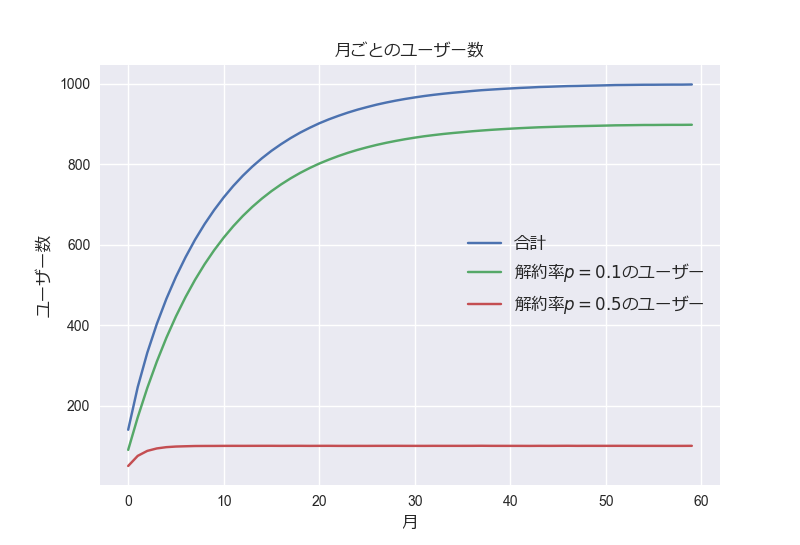
解約率は初月の新規ユーザーしかいないときの値からどんどん下がっていってある値に収束している
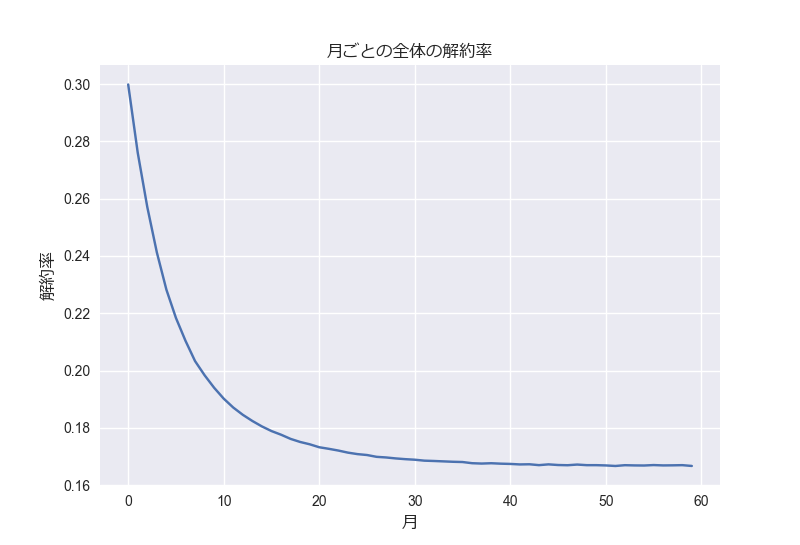
全体の解約率から計算したLTVと各ユーザーの解約率から計算したLTVの平均もグラフにした
どちらも初月の新規ユーザーしかいないときの値よりも増加している

以上のように毎月の新規ユーザーのLTVを固定してシミュレーションしても、ユーザー全体のLTVはその値とは違ってくる
おもしろいことに、収束したときの全体の解約率から計算したLTVと、新規ユーザーのそれぞれの解約率の逆数を使って計算したLTVの平均は一致しているように見える
数式的な話
ある月に残っているユーザー数は、1ヶ月目のユーザー、2ヶ月目のユーザー、……となるので、解約率と毎月契約する人数を一定とした場合、幾何級数の総和でだいたいの値が計算できます
つまり解約率\(p\)のユーザーが1ヶ月目からnヶ月目までいるときのそれらのユーザーの人数の総和は元の人数の\((1-p)\frac{1 - (1-p)^n}{1-(1-p)}\)倍となり、\(n\)が無限大になったときに収束するのは\(\frac{1 - p}{p}\)倍となります
試しに\(p=\frac{1}{10}\)を入れると\(\frac{1 - 0.1}{0.1}=9\)倍となり、上のシミュレーションの結果と一致します
この結果を使うと解約率やLTVの収束する値も計算できます
収束したときの解約率は以下のようになる
$$p = \frac{\mathrm{解約率が0.1のユーザー数} \times 0.1 + \mathrm{解約率が0.5のユーザー数 \times 0.5}}{\mathrm{解約率が0.1のユーザー数} + \mathrm{解約率が0.5のユーザー数}}$$ 今回使った解約率の定義では上のユーザー数の式とは違ってその月に解約した人数も含める必要があるので初項は最初の人数の\(1-p\)倍ではなく\(1\)倍になる。すなわち\(n\)が極大になったときに収束するユーザー数は元の\(\frac{1}{p}\)倍である
この結果を使うと以下のようになりシミュレーションの結果とほぼ一致する
$$\frac{\frac{1}{0.1} \times 100 \times 0.1 + \frac{1}{0.5} \times 100 \times 0.5}{\frac{1}{0.1} \times 100 + \frac{1}{0.5} \times 100} = \frac{100 + 100}{\frac{1}{0.1} \times 100 + \frac{1}{0.5}\times 100} \approx 0.17$$ ちなみに上の式は毎月の新規ユーザーごとの解約率の調和平均の形になっている
LTVは解約率の逆数に月ごとの金額をかければいいので収束したときのLTVの計算は上の結果を使えばよく、以下のようになる
$$1000 \times \frac{\frac{1}{0.1} \times 100 + \frac{1}{0.5}\times 100}{100 + 100} = 6000$$
この数値は新規ユーザーだけ見たときの、ユーザーごとの解約率の逆数を使って計算したLTVの平均と一致している
$$\frac{1000 \times \frac{1}{0.1} \times 100 + 1000 \times \frac{1}{0.5} \times 100}{100 + 100} = 6000$$
もう一度グラフをみると、青い線の最初と緑の線の最後が一致しているのがわかる

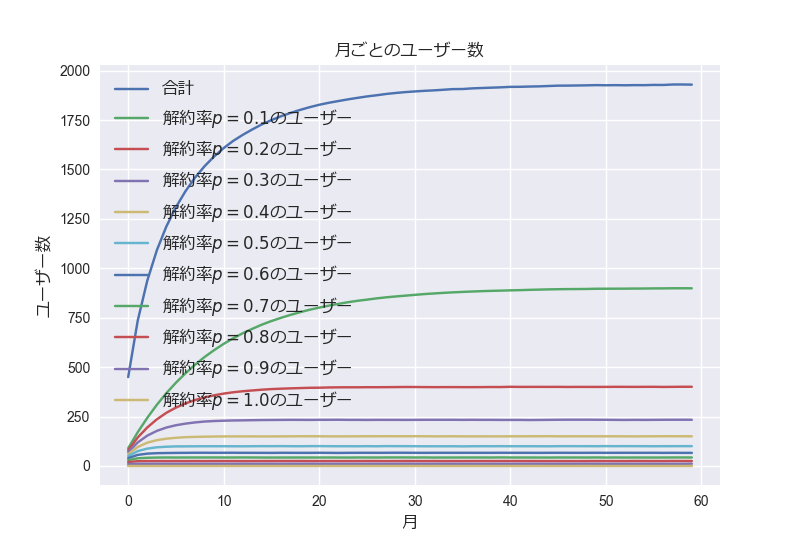
この性質が群が増えても同じような感じになるのか確かめるために解約率0.1から1.0までの10個のグループに対してシミュレーションを行いました
(グループ数以外は同様の条件で、毎月100人ずつ新規ユーザーを追加しています)
すると同様に収束した全体の解約率から計算したLTVと新規ユーザーの個々のLTVの平均がほぼ一致する結果が得られました(数式的にそうなっているので当然の結果かも)

まとめ
というわけで当然といえば当然ですが、シミュレーションで新規ユーザーの解約率が一定でも全体の解約率は新規ユーザーの解約率とは全然違う値になることがわかりました
つまり全体の解約率からLTVを計算しても新規ユーザーのLTVの推定としてはあまりよくないのかもと思うのですが、毎月同質の新規ユーザーが来るという仮定のもとでは収束するまで時間が経てば全体の解約率から計算したLTVと新規ユーザーのそれぞれのLTVを平均したものが同じ結果になるので、本当に求めたいものなのかはよくわかりませんが推定としてはそれなりによいものが出てくるのかもしれません(?)(そもそも解約率などが一定という仮定がどうなのかという話はさておき)
LTVの計算や統計についてそれほど詳しいわけではないので、誤りや知っておいた方がよい情報などあればコメントしていただけると嬉しいです
参考
Customer lifetime value - Wikipedia
Wikipediaを見るともう少し頭を使った(?)LTVの計算がいろいろあるみたいです
ソースコード
# coding: utf-8 from __future__ import division from __future__ import print_function from __future__ import unicode_literals from future_builtins import * import random import numpy as np import seaborn as sns import matplotlib.font_manager #確率の異なるn個の群のユーザーを仮定 #それぞれ毎月per_month人ごと増えていく prob = [0.1, 0.5] per_month = [100, 100] #prob = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0] #per_month = [100] * len(prob) profit = 1000 stats_user = [] stats_ratio = [] stats_ltv = [] for i in xrange(1000): stats_user.append([]) stats_ratio.append([]) stats_ltv.append([]) users = [0] * len(prob) for j in xrange(60): denominator = sum(users) + sum(per_month) for u in xrange(len(users)): users[u] += per_month[u] decrease = [0] * len(users) for u in xrange(len(users)): for v in xrange(users[u]): if random.random() < prob[u]: decrease[u] += 1 for u in xrange(len(users)): users[u] -= decrease[u] stats_user[i].append([sum(users)] + users) ratio = sum(decrease) / denominator stats_ratio[i].append(ratio) ltv = [] for u in xrange(len(users)): ltv.append(profit / prob[u]) average_ltv = 0 for u in xrange(len(users)): average_ltv += ltv[u] * (users[u] + decrease[u]) average_ltv /= (sum(users) + sum(decrease)) stats_ltv[i].append([average_ltv, profit / ratio]) stats_user = np.array(stats_user) print(stats_user.mean(axis=0)) stats_ratio = np.array(stats_ratio) print(stats_ratio.mean(axis=0)) stats_ltv = np.array(stats_ltv) print(stats_ltv.mean(axis=0)) prop = matplotlib.font_manager.FontProperties(fname=r'C:\Windows\Fonts\meiryo.ttc', size=12) sns.plt.title('月ごとのユーザー数', fontproperties=prop) sns.plt.xlabel('月', fontproperties=prop) sns.plt.ylabel('ユーザー数', fontproperties=prop) sns.plt.plot(stats_user.mean(axis=0)) sns.plt.legend(['合計'] + ['解約率$p={}$のユーザー'.format(p) for p in prob], prop=prop) sns.plt.show() sns.plt.title('月ごとの全体の解約率', fontproperties=prop) sns.plt.xlabel('月', fontproperties=prop) sns.plt.ylabel('解約率', fontproperties=prop) sns.plt.plot(stats_ratio.mean(axis=0)) sns.plt.show() sns.plt.title('月ごとのLTV', fontproperties=prop) sns.plt.xlabel('月', fontproperties=prop) sns.plt.ylabel('LTV', fontproperties=prop) sns.plt.ylim(0, 10000) sns.plt.plot(stats_ltv.mean(axis=0)) sns.plt.legend(['ユーザーそれぞれの解約率の逆数で計算したLTVの平均', '全体の解約率の逆数を使って計算したLTV'], prop=prop) sns.plt.show()