複数ラベルの分類問題を評価しようと思ってMean Average Precisionを計算しようと思ったが、Pythonの機械学習ライブラリのscikit-learn(sklearn)にはaverage_precision_score()関数とlabel_ranking_average_precision_score()関数があってどういう違いがあるのかドキュメントを読んでもいまいちよくわからなかったので調べました
とりあえず最初に結論を書いておくと、複数ラベルの分類問題でよく使われるMean Average Precisionの計算にはlabel_ranking_average_precision_score()関数を使えばよさそう
追記: バージョン0.19からどちらも同じ挙動になったようなので注意(元々のlabel_ranking_average_precision_score() 関数と同様の計算)
リンク先のNotesの部分
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.average_precision_score.html
Changed in version 0.19: Instead of linearly interpolating between operating points, precisions are weighted by the change in recall since the last operating point.
Mean Average Precision (MAP) とは
情報検索(IR)や機械学習の分野で使われる評価尺度。スコア付きの出力について、正解のものが上位のスコアであるほど大きな値になる(0から1の値を取る) 機械学習では一つの事例に複数の正解ラベルがつけられているmulti labelのタスクで用いられているのを見かけるPrecisionとRecall
最初にPrecisionとは何かについて軽く説明します 機械学習などのシステムでデータを目的のラベル(正例)とその他のラベル(負例)に分類する時、正例と判定したもののうち実際に正例だったものの割合がPrecisionです $$\text{precision} = \frac{|\{\text{正例と判定されたもののうち実際に正例であったもの}\}|}{|\{\text{正例と判定されたもの}\}|}$$ 単純な正解率ではなくPrecisionを使って嬉しい時は、例えばデータ中の目的でないラベル(負例)の比率が非常に大きい場合に全部を負例と分類しても高い正解率になってしまう場合などがあります 逆にシステムが正例と判定したものが、評価用のデータセットの正例のうちどれぐらいの割合をカバーしているのかを示す評価尺度もあり、これはRecallと呼ばれます $$\text{recall} = \frac{|\{\text{正例と判定されたもの}\}|}{|\{\text{データセット中に含まれる正例}\}|}$$ Precisionが正確さ、Recallがカバー率的なものを表していますAverage Precision
次にAverage Precision (AP) について説明します Average PrecisionはPrecisionをRecallについて平均をとったものです PrecisionとRecallを軸にしてPrecision-Recall curveのグラフを書いたときの曲線以下の部分の面積(AUC, Area Under the Curve)がAverage Precisionになります(以下のグラフだと折れ線ですが)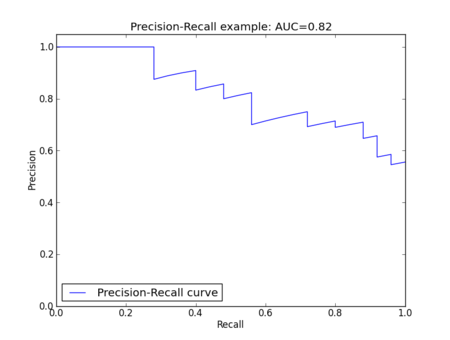
ちゃんと計算するには積分的な計算が必要になる(？)っぽいですが、近似値の計算として(？)以下のような式が使われているのをよく見かけます
出力をスコア上位順に並べた時にk番目の出力が正例なら1、負例なら0になる関数を\(I(k)\)と定義した時
$$\text{Average Precision} = \frac{\sum_k \text{k番目までの出力で計算したPrecision} \times I(k)}{|\{\text{データセット中の正例}\}|}$$
複数ラベルの分類の評価ではデータの各事例ごとに、正解のラベルを正例それ以外を負例とみなしてAverage Precisionを計算します
簡単な例として以下の表のデータのAverage Precisionを計算してみます
| ラベルの種類 | ラベルがついているか(ついていれば1) | 出力されたスコア |
|---|---|---|
| 赤い | 1 | 1 |
| 丸い | 0 | 0.8 |
| 重い | 1 | 0.6 |
| 辛い | 0 | 0.4 |
scikit-learnの関数
ようやく本題に入ります sklearnにはaverage_precision_score()関数とlabel_ranking_average_precision_score()関数という似たような名前の関数があり、どちらを使えばよいのかちょっと混乱しました ドキュメントを見ると、両方共適切な引数を渡せばMAPが計算できそうですが実行してみると違う値になりますfrom sklearn.metrics import label_ranking_average_precision_score, average_precision_score average_precision_score([1, 0, 1, 0], [1, 0.8, 0.6, 0.4], average='samples') #0.79166666666666663 label_ranking_average_precision_score([[1, 0, 1, 0]], [[1, 0.8, 0.6, 0.4]]) #0.83333333333333326よくわからなくなってきたのでソースコードを読んで調べてみました すると以下の式の定義と等しい計算をしていそうなのはlabel_ranking_average_precision_score()関数の方でした $$\text{Average Precision} = \frac{\sum_k \text{k番目までの出力で計算したPrecision} \times I(k)}{|\{\text{データセット中の正例}\}|}$$ 上の式では実は面積を以下の画像のように長方形で近似して計算しています
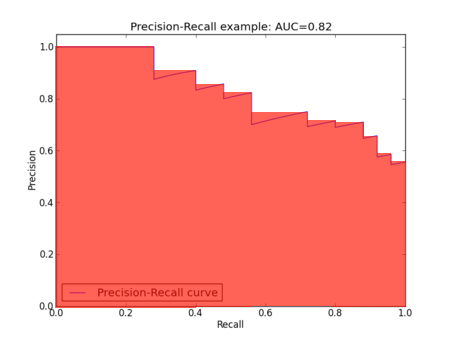逆にaverage_precision_score()関数の方では、numpy.trapz()関数を使って面積の計算を台形で近似して計算していました
つまりある意味average_precision_score()関数の方が正確な計算をしているということになります
不勉強のためAverage Precisionの定義として以下のような定義しか知らなかったのですが、実際には以下の式は近似値の計算をしているということっぽいです
$$\text{Average Precision} = \frac{\sum_k \text{k番目までの出力で計算したPrecision} \times I(k)}{|\{\text{データセット中の正例}\}|}$$
まとめ
multi label classificationの評価尺度としてMean Average Precisionを計算したいときはlabel_ranking_average_precision_score()関数を使えばよい(上位k件の出力までしか見ない@kの機能は今はついてなさそう) scikit-learnのaverage_precision_score()は台形で計算しているので、よく使われるAverage Precisionの式とは少し違う値になる ちなみに完全に今更ですが、scikit-learnもnumpyもドキュメントにソースコードへのリンクがついていて便利なことに気づきました
